Windtunnel Design & Construction – part 5: the contraction duct

The geometry of the contraction duct is to be defined by the following constraints:
-a horizontal tangent at both ends of the curve (first derivative equals zero here)
-an inflection point half way
-degree of curvature decreases to zero at both ends of the curve (second derivative equals zero)

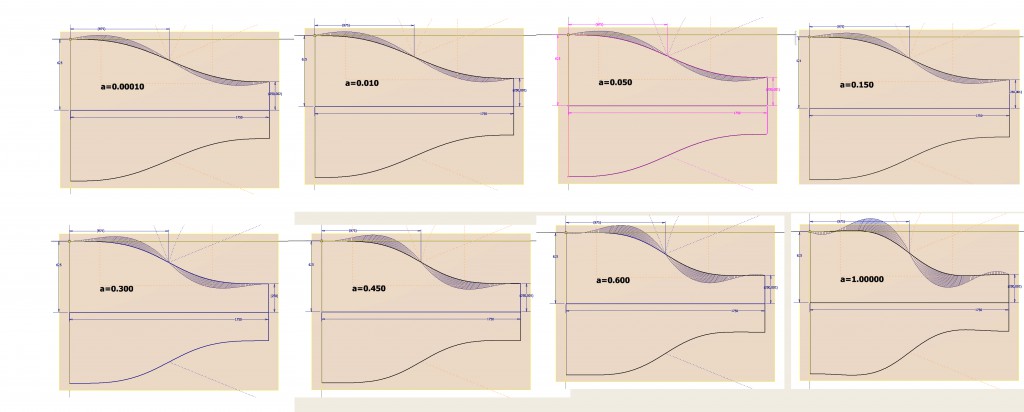
Deriving an equation for half of the curve of the  walls, with the depth L of the contraction duct being 1750mm , Inlet dimensions of 1750mmx1250mm and outlet dimensions of 700x500mm, results in:

X=875*t
Y=875*(A*t^2-7*A*t/3 +B*t +4*A/3 -2*B)*(t^3)

with B= 0.3 for the side walls and B=0.214286 for the top and bottom walls.

Parameter A defines the ‘aggressiveness’ of the change in curvature.

[BELL] provides Y(X)= Hi- (Hi- He)6(X’)^5 – 15(X’)^4 + 10(X’)^3 as the equation that resulted in the best performing contraction duct,
with
Hi = contraction height at inlet
He = contraction height at outlet
and L/Hi > 0.89

It can be shown that the derived equation, used to design the geometry in the 3D-model, is equivalent to the Bell-equation for a value of A = ~ 0.000001

The contraction duct is the largest single part of the wind tunnel, weighing in at 320kg. The part is also designed to be 10mm smaller and 100mm lower than the door of the wind tunnel room.

The outer frame, composed from 6mm lasercut steel, was assembled first and tack welded. This structure defined the geometry of the contraction duct.
The 2mm wall panels were then positioned inside the structure, bent outward against the frame and tack welded.

Looking down into the upright contraction duct. The plywood slats are being used to push the wall sheets outwards against the frame.
 

The assembled contraction duct, suspended on winches in the Antwerp workshop.

Details of the tack welds.